Snakes on a plane
 (圖片來源: IMDB)
(圖片來源: IMDB)
兩年前有部災難片(還是恐怖片), 叫做 Snakes on a plane(飛機上有蛇)。你曉得的, 這種片子就像周星馳在食神裏說的一樣: 味道有多重加多重,飲料冰塊有多少放多少,吸管有多粗用多粗。反正不是數量多到你頭皮發麻, 就是怪物大到讓你肝膽俱裂。
這就是陳之藩名句: "數" "大" 便是美 的最高深境界啊!!
同一時間, Al Zimmermann 有一個找尋最佳解的競賽, 總獎金為500 塊美金(眼睛亮起來了嗎??很抱歉, 兩年前比賽就結束了)。當年我也有看到這則訊息, 但是到網站上看了看後, 實在搞不清楚它在幹什麼, 還以為是電影公司在搞噱頭。
為什麼會扯到電影, 很簡單, 因為這個比賽名字也叫做 Snakes on a plane。不過電影中的 Plane 是指飛機, 而這裏的 Plane 則是指平面, 也就是你要在一個限制的平面中, 依他的規則, 找出最大可能性的長度。
直到最近再看了一次, 才恍然大悟 – 原來是這麼一回事啊~~
其實這個謎題要追溯到 Serhiy Grabarchuk 所構想的一道題目 Neo Matchstick Snake。Grabarchuk 是個愛好謎題的家族, 他們的謎題也都出得很漂亮, 我手上有一本 Puzzle Classics, 還真的是夠經典。
來說明一下 Neo Matchstick Snake。先想像一下, 你現在有一個2x2大小的正方形範圍, 還有一堆的火柴棒, 而這些火柴棒長度一樣, 都是1。現在請你將火柴棒一根接一根放在這個正方形範圍中, 相鄰火柴棒間的角度必須是45, 90, 135或180 其中之一, 但火柴棒不能交叉穿越其他火柴棒, 也不能碰到(但最終的尾巴連到開始的頭, 形成一個環, 是可以被接受的)。現在的問題是: 你到底能接多長??
想像一下, 假設是這樣…
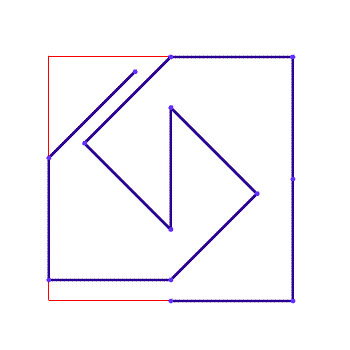
(這條蛇的長度為12)
當然這並不是最長的, 似乎目前為止 Jeremy Galvagni and Bob Wainwright 找到的15是最佳解。而 Roger Phillips 不但找到了15的長度, 連圖形旋轉180度後還是一樣。

(Jeremy Galvagni and Bob Wainwright 答案, 圖片來源: Mathpuzzle)

(Roger Phillips 答案, 圖片來源: Math Magic)
所以就這麼完了嗎??當然不!!就如同有一堆變態的出題者會把 Sudoku 和 Battleship 搞出一堆的變體, 這麼優的題目構想怎麼會如此就收尾呢??
2003年5月在 Math Magic 網站的討論, 就用這個題目當每月一題的構想。其實我們看原先的發想, 可以發現到轉折的角度基本上就是45的倍數。
所以它的第一題是:
1. 如果轉折角度是45的倍數, 可以多長??
2. 如果轉折角度是30的倍數(如30,60,90,120,150,180), 可以多長??
3. 如果轉折角度是22.5的倍數(如 22.5, 45, 67.5, 90, 112.5…etc), 可以多長??
而第二題就完全地逆轉, 變成『如果要限定轉折角度為x 度, 長度為 n 的蛇所能放在的正方形範圍, 邊長最小為多少』, 然後再調整 x 及 n 做討論
接下來再增加一個條件: 要是這條蛇的頭尾必須相接形成環狀, 那麼不同情況下, 正方形範圍的邊長最小又是多少??
之後再討論: 那要是在長方形呢, 情況會如何??在三角形呢??五邊形呢??六邊形呢??又有什麼樣的情況??
最終章 – 要是這條蛇在立體的空間…
 (圖片來源: Math Magic)
(圖片來源: Math Magic)
真的是夠了, 我可以想像這條立體空間的蛇做出比印度眼鏡蛇, 更高難度的瑜珈動作(你去想像一條蛇扭腰擺臀, 擠在小小的空間中, 重要的是每個轉折長度還一樣), 我可以去告設計這道題目的人在虐待動物嗎??
這時我們就可以回到 Al Zimmermann's Programming Contests 了。
這個題目限制的範圍不再是正方形, 而是一個圓。題目要你找出每種組合的最長值(如給定n 和 D 值, 轉的角度為180/n 的倍數, 而蛇必須在直徑為 D 的圓內)

(圖片來源: Al Zimmermann's Programming Contests )
然後這裏的網頁還可以做線上測試, 輸入數字就可以檢驗蛇的狀況。
至於怎麼輸入數字, 就是先輸入 n 值後, 再依續輸入每次轉折的角度方向。不過有點難解釋和翻譯, 所以就直接請看英文原文吧…
-(我是快樂的分隔線)-
為什麼會去談這個題目呢??因為它真的是一個還蠻棒的多解題。現行的教育體制中, 我們不斷地在強調創意, 要學生學到解決問題的能力。但只要一碰到升學, 答案就恢復成只有一個。這道題目最可貴的是, 簡單的規則, 卻有著無窮的變化, 永無止境的挑戰, 讓它像一道陳釀的女兒紅, 越久越能享受到它的芬芳。雖然比較可惜的是它的思維模式可能對國中生來說比較複雜, 畢竟要去算一些轉折特定角度的距離, 是有點麻煩。但也或許我們可以提供像下面的數字:
sin30°= 0.5
cos30°= 0.866
sin45°= cos45°=0.7071
……
看不懂cos 或 sin 就用下面這種圖好了…
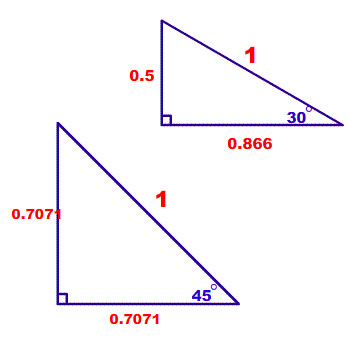
也可以讓他們要去說明他們排列出的那條蛇,『的確』 會落在範圍中, 自己去思索並檢驗答案的正確性。
至此, Snakes on a plane, 就不再只是個災難恐怖片, 而是有無限可能的擺放題目。
又或者, 對某些學生來說, 它仍然是個災難…??:P


回應文章建議規則: