PuzzleUp 2008 討論系列5 – 疊床架屋 Part I
這是一篇充滿了『圖』的文章…
發布日: October 29, 2008
國中時參加過一個營隊。
你知道的, 營隊不外乎就是那些元素 – 大哥哥大姐姐, 很多你喜歡和不喜歡的人, 一堆現在看起來很幼稚的團康, 外加最後哭到生離死別的晚會。
記得有個團康是這樣子玩的, 當時我們在闖關…
關主:『每個人脫掉一隻鞋子。』
於是地上出現了各色的鞋子, 還有的霸凌爬到人家頭上。
關主:『把鞋子依間隔距離排好。』
鞋子們排好隊, 準備升旗唱國歌…
遊戲開始了, 每個人要輪流上場(輪完可以再輪), 做什麼??
跳鞋子…不過是單腳。
在單腳的狀況下, 你要依序跳過鞋子隊伍。可以隨時停, 然後你就把你跳過的鞋子都拿回去, 再換下一個人。但有個條件, 要是你踩到了鞋子, 那麼即使之前跳過的也不能拿走, 自己得摸摸鼻子回到隊伍最後等下一輪。
每個人都想當英雄, 大家心裏想的大概是類似的:『要是我一個人可以跳完全程, 拿回所有的鞋子, 不就馬上就過關了嗎??』
公布中場結局 – 所有人都輪過了, 但一隻鞋子都沒回來。
終於這時候有個人醒了 – 我們應該從近的鞋子拿起啊, 跳一隻就停, 拿回一隻。每拿走一隻, 前面的路也清空了。這樣會不會比較快?
兩分鐘不到, 所有的鞋子都回到主人腳上了。
從簡單的做起, 每一步都讓下一步有根基, 更容易。也許會花點時間做容易的事, 卻能更快解決問題。我們來看這道題目。
--
Height Row
(圖片來源: PuzzleUp 網站)
You will place 16 people with different heights to a meeting room with a 4x4 (square array) arrangement of seats such that each person will be taller than both the person in front of and left to her/him.
你要安排16個身高不同的傢伙坐在會談室, 座位排成如4x4 的方陣。而每個人都要比在他前方或左方的人來得高。
In how many different ways can this operation be carried out?
你有幾種排法??
If the question was for 9 people and a 3x3 arrangement of seats, then the answer would be 42.
假如這個問題改成9個傢伙坐在3x3的座位時, 答案會是42。
呃, 好吧!!我們將這些人從矮到高編號1-16(最矮的是1, 而16是最高的)。想想看每個位子可能坐哪些人…
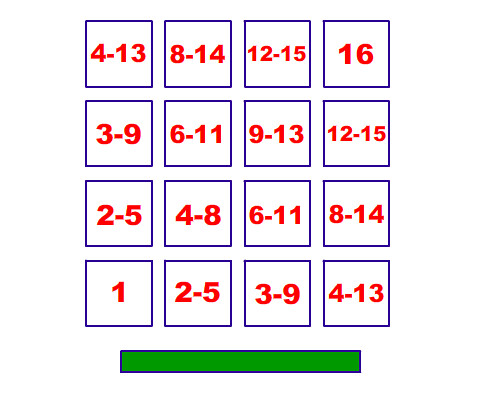
然後我們得到一個結論 – 這種做法完全沒用!!因為你不可能把所有可能性相乘。
那我們也許可以試著一個一個去放…
首先是第一個人(其實16也可以直接放)
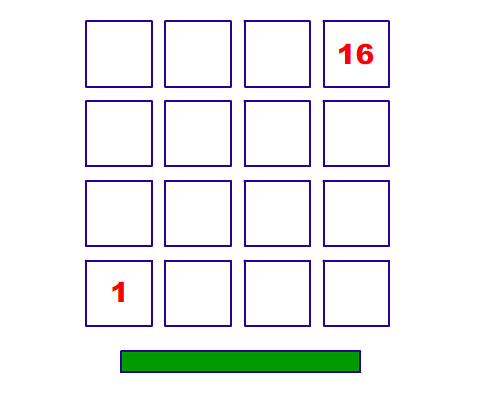
再來是第二個人, 第二個人雖然有兩種放法, 但我們只要去思考其中一種, 再將最後答案乘以2就好了, 因為另一種只是45度角的鏡射。
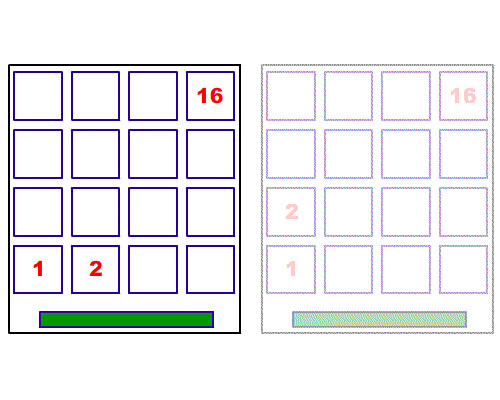然後第三個人…
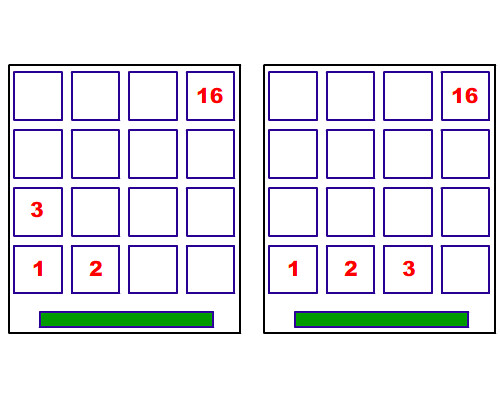
第四個人…呃, 好像方式繁殖得有點快…
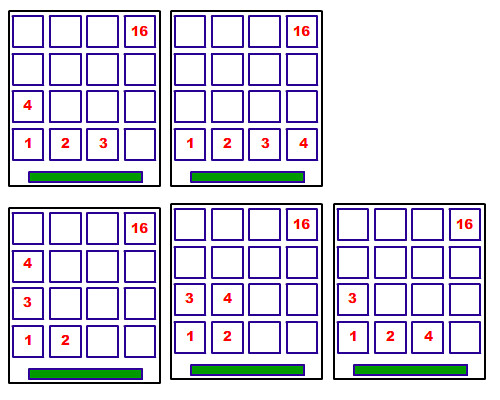
第五…『老子不幹了!!』, 比黃金鼠還會生。
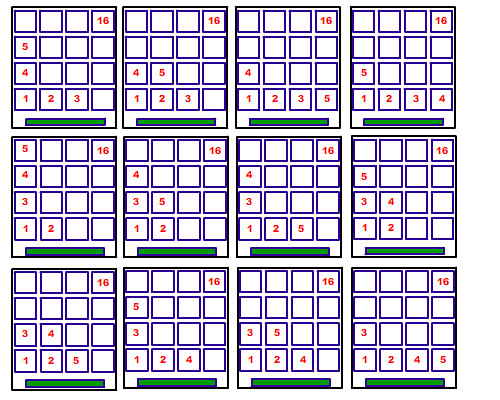
顯然這也不是個好方法。你可能要有很大張的紙, 配上如証嚴法師的脾氣。
我們很期待可以一步就做完, 順順利利一路做下去, 但是事與願違。也許我們該從3x3去思索, 它是怎麼算出42的。
不過你還記得嗎??3x3 有9個人, 但是我剛才到了第5個人就凍未條了。
也許該再更少一點, 像是…2x2??
或乾脆一點, 反正圖的版面夠, 把2-4的可能性都畫出來好了。
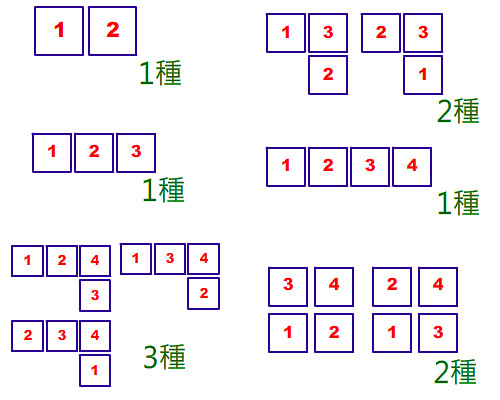
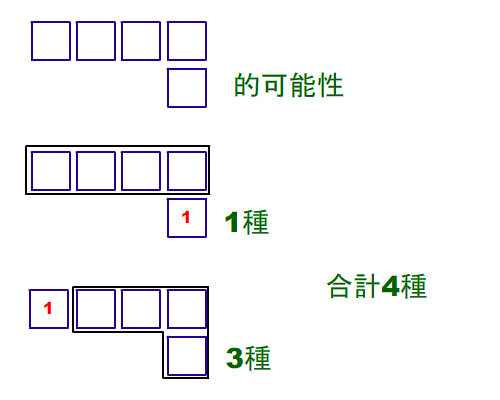
然後是5格, 你就可以先放入1後, 再依剩下圖形來看有幾種可能。你不用再重新數, 因為4格的可能性有幾種你都算出來了。
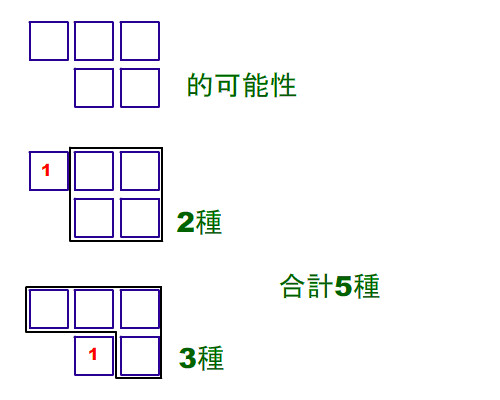
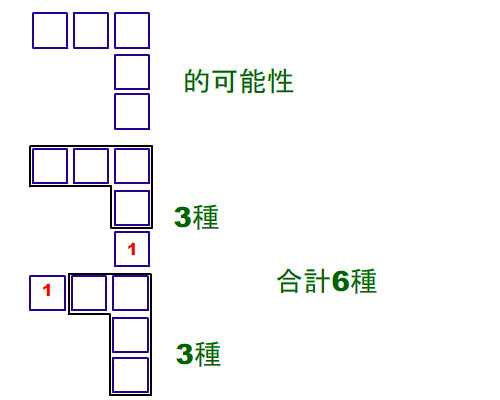
接著6格, 我就舉其中一例來說明就好了-
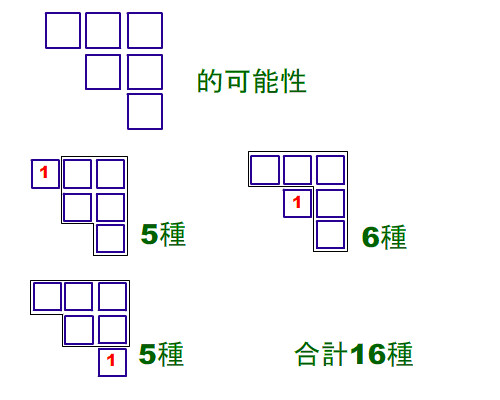
也許你會認為到後面數字越多, 會不會有漏掉可能性的情況。
其實不會, 有三個原因 –
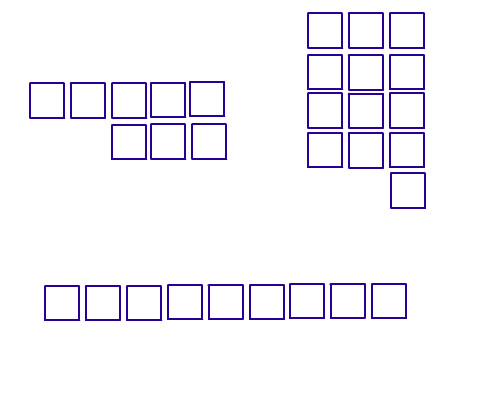
1. 有些圖形根本不用列入考慮
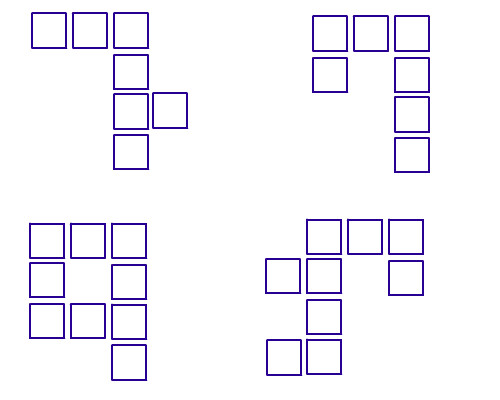
基本上放的過程中, 上面一定比下面來得晚放, 右邊一定比左邊來得晚放, 而我們到了最後, 是要檢查剩餘格子的, 所以不可能有以上的情況發生。
2. 邊界只有四格, 所以可能性會減少很多
不會發生像上面的圖形
3. 就算漏掉了, 因為我們是依圖形的區域來做統計, 所以不會有關係。而且到了下一步, 你自然會發現。
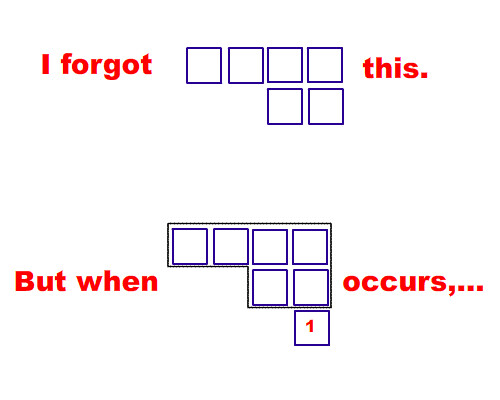
像是可能我們漏掉了6的其中一種可能, 但是當我們要到7格時, 自然就會發現缺了這個資訊, 要補也還來得及。
基本上到12就差不多了。
剩下的就用以下的圖形, 依序分析有幾種, 再加起來。
當然, 不要忘了最後答案還要再乘以2, 用來表示2位置的45度鏡射。
萬丈高樓平地起, 我們就這樣一層一層地搭, 每蓋一層樓, 都是為了下一層樓打基礎, 讓它有穩固的平面可以支撐。
最終, 我們完成了這個答案。
回應文章建議規則：